日志
原题可见:《奥数比赛,难题求解(一) --- 题目》
题解可见:《奥数比赛,难题求解(二) --- 题解》
中间证明:《奥数比赛,难题求解(三) --- 证明中间条件》
至此,我们还有两条有待证明:1)QHMA’四点共线;2)。KHQ’三点共线;
题解可见:《奥数比赛,难题求解(二) --- 题解》
中间证明:《奥数比赛,难题求解(三) --- 证明中间条件》
至此,我们还有两条有待证明:1)QHMA’四点共线;2)。KHQ’三点共线;
证明:
我们先来证明2)。KHQ’三点共线;这是显而易见的,如上图,因为:QQ’是直径,所以,∠Q’KQ=90°,根据条件:∠HKQ=90°,而过K一点和KQ垂直的直线只有一条,所以,KHQ’三点共线;证毕。
同理可证:1)QHMA’四点共线中,QHA’三点共线;下面证明:M在QHA’上。
如图,注意到四边形BA'CH是平行四边形,M是对角线BC的中点,必然是另一条对角线HA’的中点,所以A’MH共线。要证明BA'CH是平行四边形,只须证明:
∠A’BC=∠HCB,和∠A’CB=∠HBC,和事实上:我们有:
∠A’BC=∠HCB :
∠A’BC=90°-∠ABC(因为AA’是直径)=∠BAD(∠AFB=90°)=∠BCD(圆周角定理)=∠HCB(ΔCHF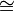 ΔCDF)
ΔCDF)
∠A’CB=∠HBC:∠A’CB=90°-∠ACB=∠CAD=∠CBD=∠HBC
证毕。
至此,全部题目证明完毕。我们将用综合法,再写一个统一的题解。










